Formulas of Common Geometric Shapes

Geomatric Shapes Formula

Formulas of Common Geometric Shapes

(2D and 3D) (With Diagrams)

(Easy GK Notes for School & Competitive Exam Students)

Understanding basic geometry shapes is important for GK, Maths, and entrance exams. Below are simple formulas with diagram examples to make learning easy.

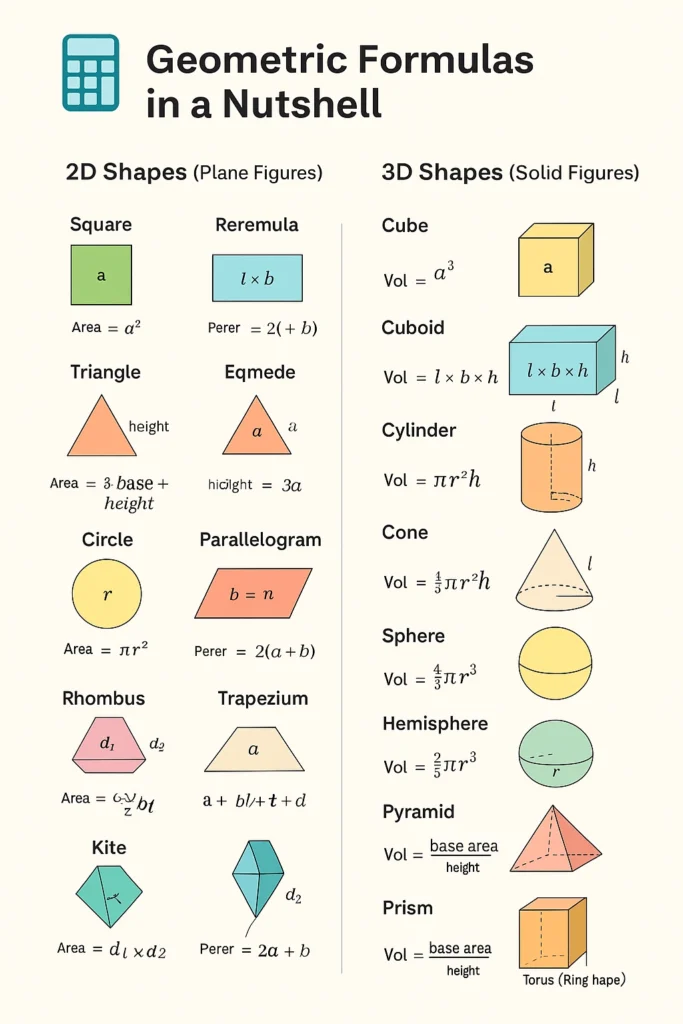
🟩 2D Shapes (Flat Figures)

Shape	Diagram	Formula
Square	⬜	Area = a² Perimeter = 4a
Rectangle	▭	Area = l × b Perimeter = 2(l + b)
Triangle	🔺	Area = ½ × base × height Perimeter = a + b + c
Circle	⚪	Area = πr² Circumference = 2πr
Parallelogram	▰	Area = base × height Perimeter = 2(a + b)
Trapezium (Trapezoid)	⏢	Area = ½ × (sum of parallel sides) × height

Formula for Common Geometric Shapes

🟦 3D Shapes (Solid Figures)

Shape	Diagram	Formula
Cube	◼️	Volume = a³ Surface Area = 6a²
Cuboid	📦	Volume = l × b × h Surface Area = 2(lb + bh + hl)
Cylinder	🧯	Volume = πr²h Surface Area = 2πr(h + r)
Cone	🍦	Volume = ⅓πr²h Surface Area = πr(l + r)
Sphere	⚽	Volume = ⁴⁄₃πr³ Surface Area = 4πr²
Hemisphere	🥣	Volume = ⅔πr³ Surface Area = 3πr²

Quick Tips for Students:

Use π = 3.14 or 22/7.
Area is always in square units (cm², m²).
Volume is in cubic units (cm³, m³).
Draw and label shapes while learning to avoid confusion.

Formula for Common Geometric Shapes

Formula in Nutshell

Algebra Formulas

Formula Type	Formula
(a + b)²	a² + 2ab + b²
(a − b)²	a² − 2ab + b²
a² − b²	(a + b)(a − b)
(a + b + c)²	a² + b² + c² + 2(ab + bc + ca)
(a + b)³	a³ + 3a²b + 3ab² + b³
a³ + b³	(a + b)(a² − ab + b²)
a³ − b³	(a − b)(a² + ab + b²)

Tip for Exams

Memorize π = 22/7 or 3.14
Know Pythagoras Theorem: a² + b² = c²
Learn unit conversions:
- 1 km = 1000 m
- 1 m = 100 cm
- 1 litre = 1000 ml

Geometry Formulas (3D Shapes / Mensuration)

Solid Shape	Diagram	Volume	Surface Area
Cube	⬛	a³	6a²
Cuboid	📦	l × b × h	2(lb + bh + hl)
Cylinder	🧯	πr²h	2πr(h + r)
Cone	🔺 (3D)	(1/3)πr²h	πr(l + r) where l = √(r² + h²)
Sphere	⚽	(4/3)πr³	4πr²
Hemisphere	⚪⬇	(2/3)πr³	3πr² (TSA), 2πr² (CSA)

📘 Trigonometry (Basic)

Ratio	Formula
sinθ	Perpendicular / Hypotenuse
cosθ	Base / Hypotenuse
tanθ	Perpendicular / Base
cotθ	1 / tanθ
secθ	1 / cosθ
cosecθ	1 / sinθ

Important Identities:

sin²θ + cos²θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = cosec²θ

Pythagoras Theorem (पाइथागोरस प्रमेय) – आसान भाषा में समझिए

📘 परिचय (Introduction)

पाइथागोरस प्रमेय (Pythagoras Theorem) गणित का एक बहुत ही महत्वपूर्ण सूत्र है, खासकर त्रिभुज (Triangle) के अध्याय में।
यह प्रमेय केवल समकोण त्रिभुज (Right-Angled Triangle) पर लागू होता है।
यह प्रमेय प्राचीन यूनानी गणितज्ञ पाइथागोरस (Pythagoras) द्वारा खोजा गया था।

पाइथागोरस प्रमेय क्या कहता है? (What the Theorem Says)

हिंदी में:
किसी समकोण त्रिभुज में, कर्ण (Hypotenuse) की लंबाई का वर्ग, अन्य दो भुजाओं (Base और Perpendicular) के वर्गों के योग के बराबर होता है।

English Version:
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides (base and perpendicular).

Formula (सूत्र)

Hypotenuse2=Square of Base +Square of Perpendicular

Pythagorus